مبنای دودویی کامپیوتر | 0 و 1 در کامپیوتر چیست؟

تعریف مبنا در ریاضی

اعداد باینری اهمیت فراوانی در علم کامپیوتر دارند

در علم ریاضی مبنا (نام های دیگر آن پایه و بیس است) یعنی تعداد رقم های فردی مع برای نوشتن یک عدد در دستگاه عددنویسی ارزش مکانی بکار می برند. به عنوان مثال، در سیستم عددنویسی ده دهی که امروزه تبدیل به یکی از رایج ترین دستگاه های شمارش در جهان شده است، از ده رقم صفر تا نه استفاده می کنیم، بنابراین پایه یا مبنا این دستگاه ده است. بیشتر اعدادم معمولی که در زندگی روزمره استفاده می کنیم بر مبنای ده است اما در علم کامپیوتر نه. این مقاله توسط وبسایت چهارراه کامپیوتر تهیه شده است.

مبنا در علم کامپیوتر

 مبنای مورد استفاده در محاسبات رایانه مبنای دودویی است که در ادامه به آن می پردازیم.

دستگاه اعداد دودیی

دستگاه اعداد دودویی یا همان مبنای دودویی (دورین، باینری) هر عدد را با دو رقم صفر و یک نشان می دهد. به این نمایش، نمایش اعداد در مبنای دودویی می گوییم.

روش تبدیل مبنا ها در کامپیوتر و خواندن اعداد باینری

روش تبدیل مبناها در کامپیوتر چگونه است؟ به دو حالت مبنا ها را می توانیم تبدیل می کنیم. از ده دهی به مبنای دودویی و برعکس از مبنای دودویی به ده دهی.در هر حالت نحوه خواندن اعداد باینری را هم توضیح می دهیم.

حالت اول: از ده دهی به دودویی

یک روش بسیار ساده و معمول تبدیل مبنای ده دهی به دودویی متوالی تقسیم کردن بر عدد 2 است و باقی مانده های بدست آمده از این عملیات را تا رسیدن خارج قسمت به عدد صفر تقسیم می کنیم. در پایان، آخرین خارج قسمت و باقی مانده بدست آمده را از آخر به اول در کنار هم می نویسیم. عددی که بدست می آید یک عدد در مبنای دودویی است.

حالت دوم: از دودویی به ده دهی

اول از همه ارزش مکانی اعداد را حساب می کنیم به این صورت که عدد اول از سمت راست در جایگاه دو به توان صفر است و عدد دوم در جایگاه دو به توان یک و همینطور تا آخر. بعد هر کدام از این اعداد را در ارزش مکانی شان ضرب می کنیم و همه آنها را با هم جمع می کنیم. فراموش نکنید که باید در مبنای ده جمع کنید. عددی که بدست می آوریم در مبنای ده است و مساوی با عدد اولیه در مبنای دودویی است.

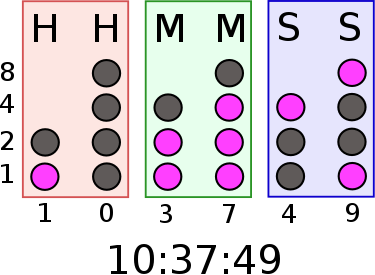
نحوه خواندن ساعت باینری

ساعت باینری زمان را بر پایه قاعده های باینری نشان می دهد. ستون اول ساعت، ستون دوم دقیقه، ستون سوم ثانیه هر ستون چهار خط دارد. مطابق شکل زیر خط اول عدد یک، خط دوم عدد دو، خط سوم عدد چهار و خط آخر عدد هشت است. ستون سمت چپ عدد دهگان و ستون سمت راست عدد یکان را نمایش می دهند که اگر اعداد هر ستون را جمع کنیم و بعد ستون ها را با هم جمع می کنیم ساعت، دقیقه و ثانیه را بدست می آوریم.

دلیل استفاده از مبنای دودویی در کامپیوتر

دلیل استفاده از مبنای دودویی در کامپیوتر؟ کامپیوترها به خاطر سخت افزار و محاسبات فیزیکی از مبنای دودویی استفاده می کنند. هر عددی که در کامپیوتر می بینید حامل یک سیگنال الکتریکی است این سیگنال ها در اندازه و قدرت های متفاوت هستند و همیشه از باینری استفاده می کنند. کامپیوترهای مدرن و امروزی از برای محاسبات باینری سنگین شان از ترانزیستورها بهره می گیرند.

کار ترانزیستور در این فرآیند این است که به جریان ورودی اجازه عبور از منبع را می دهد و آن را به سمت مصرف کننده هدایت می کند. در زمان حال، اندازه ترانزیستور ها بسیار کوچک شده و اکثر آنها تنها پنج نانومتر فضا می گیرند. در CPU های امروزی شاهد استفاده از این ترانزیستورهای کوچک هستیم.

چرا در کامپیوتر فقط از مبنای دودویی استفاده می کنیم؟

خب پاسخ اول این است که یجورایی استفاده از مبنای دودویی در کامپیوتر عادت مان شده. مسئله بعدی رقم است. با داشتن بیش از دو رقم کار ما دو برابر می شود یعنی انجام محاسبات بسیار سخت تر و وقت گیر تر می شوند. البته هنوز بیشتر سخت افزارها از عهده انجام محاسبات در سیستم های بر مبنای سه بر نمی آیند. ساخت چنین سخت افزارهایی بسیار سخت است. اولین نسخه از دستگاهی بر مبنای سه، در دهه پنجاه میلادی ساخته شد. روی کاغذ همه چیز عالی بنظر می رسید اما در عمل بازده مناسبی از خود نشان نداد. علت ضعف این دستگاه بخاطر روش کار ترانزیستورها بود. آنها برای دو ورودی یک خروجی در نظر می گرفتند و بازده سیستم پایین می آمد. همچنین این دستگاه خطا های محاسباتی فراوانی داشت و در انجام بسیاری عملیات های ریاضی باز می ماند.

اگر دستگاهی بر مبنای دودویی کار کند. دو ورودی آن چهار خروجی خواهند داشت ولی در مبنای سه خروجی ها حداقل باید نه عدد باشند. مشکل بعدی عملگر ها هستند. در باینری چهارده عملگر نیاز داریم اما در مبنای سه به بیش از هزار و نهصد عملگر نیاز است. به خاطر همین مشکلات فعلا کسی مشتاق به کار کردن با سیستم های در مبنای سه نیست. شاید روزی بتوانیم از مبنای سه هم استفاده کنیم اما در حال حاضر چنین امری بعید به نظر می رسد.

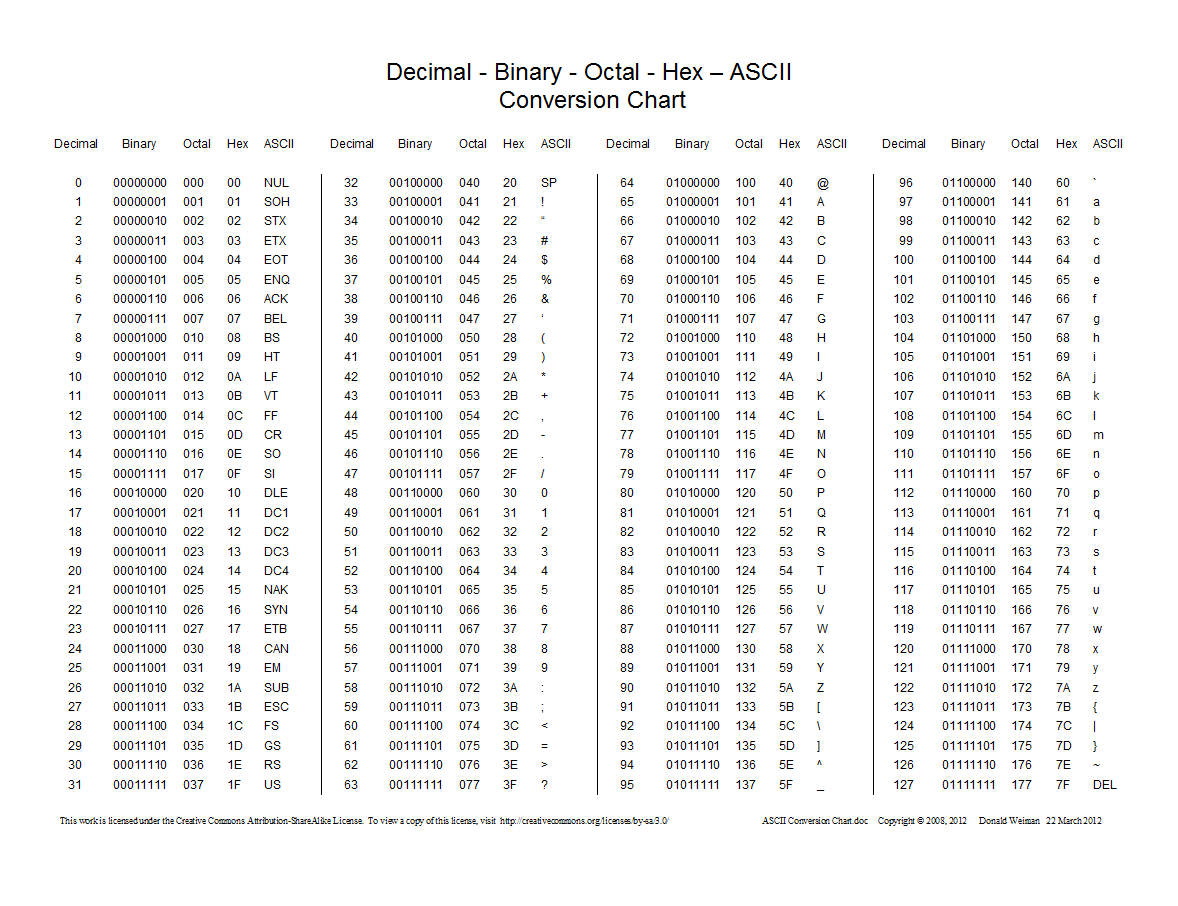
جدول باینری

در جدول باینری زیر، معادل باینری تبدیل شده به Decimal ، Octal ، Hex ، ASC2 را می توانید مشاهده کنید.